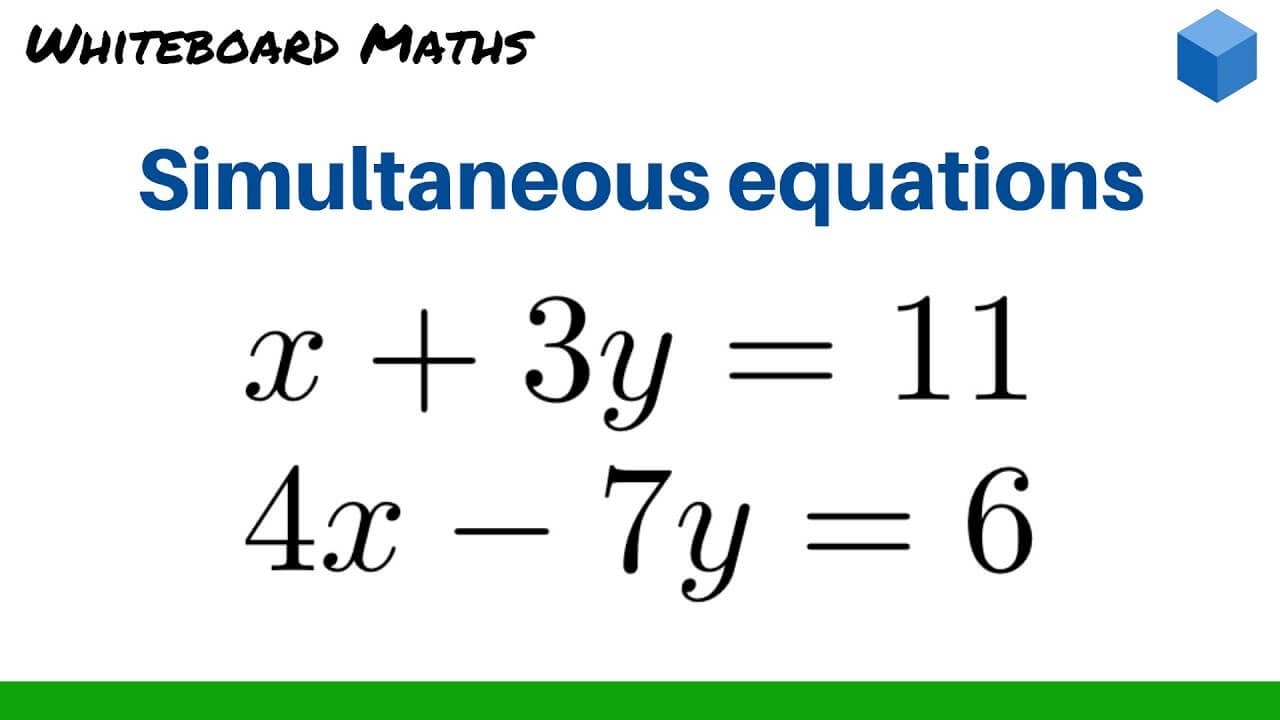Simultaneous equations are a fundamental topic in mathematics, particularly in algebra. These equations involve finding values of variables that satisfy multiple equations at once. For students and learners, mastering this concept is essential as it forms the basis for solving real-world problems and understanding advanced mathematical concepts. One of the best platforms for practicing simultaneous equations is Corbettmaths, a popular educational website that offers detailed resources for students and teachers.
This article delves into simultaneous equations, explains their types and solving methods, and highlights the resources and practice questions available on Corbettmaths. By exploring this, students can strengthen their understanding and apply their knowledge confidently in exams and real-life scenarios.
Understanding Simultaneous Equations
Simultaneous equations refer to a set of equations with two or more unknowns. The solution is a pair (or set) of values that satisfies all the equations simultaneously. For instance, solving the equations: x+y=7x + y = 7x+y=7 and 2x−y=42x – y = 42x−y=4 would require finding values for xxx and yyy that satisfy both equations at the same time. The solutions to such equations are typically found using algebraic or graphical methods.
Types of Simultaneous Equations
- Linear Simultaneous Equations: These equations consist of linear expressions. For example: 2x+y=52x + y = 52x+y=5 and x−y=2x – y = 2x−y=2. The variables appear to the first power, and the graph of these equations would be straight lines.
- Non-linear Simultaneous Equations: These equations involve at least one equation that is non-linear. For instance: x2+y2=25x^2 + y^2 = 25×2+y2=25 and x+y=7x + y = 7x+y=7. Solving these involves more complex methods, such as substitution or numerical approximations.

Methods to Solve Simultaneous Equations
- Substitution Method: In this method, one equation is solved for one variable in terms of the other. The result is substituted into the second equation to find one variable, and then the first variable is determined. Example: Solve 2x+y=102x + y = 102x+y=10 and x−y=1x – y = 1x−y=1: From the second equation: y=x−1y = x – 1y=x−1. Substitute y=x−1y = x – 1y=x−1 into the first equation: 2x+(x−1)=102x + (x – 1) = 102x+(x−1)=10. Solve for xxx, then find yyy.
- Elimination Method: This method involves adding or subtracting equations to eliminate one variable, reducing the system to a single-variable equation. Example: Solve 3x+2y=123x + 2y = 123x+2y=12 and 2x−2y=42x – 2y = 42x−2y=4: Add the equations to eliminate yyy: 5x=165x = 165x=16. Solve for xxx, then substitute xxx back into one of the original equations to find yyy.
- Graphical Method: This involves plotting the equations on a graph and finding their point of intersection. This point represents the solution. While useful for visual understanding, it may lack precision compared to algebraic methods.
Simultaneous Equations on Corbettmaths
Corbettmaths is a trusted resource for mathematics education, renowned for its quality practice questions, tutorials, and worksheets. For simultaneous equations, Corbettmaths provides an extensive range of materials tailored to different learning levels. From introductory lessons to advanced problem-solving, this platform ensures that students are equipped to handle various scenarios.
Key Features of Simultaneous Equations Resources on Corbettmaths
- Video Tutorials: Corbettmaths offers clear, step-by-step video explanations for solving simultaneous equations. These tutorials cover substitution, elimination, and graphical methods in detail, ensuring learners understand the underlying principles.
- Practice Questions: The site includes a wide array of questions, ranging from basic to challenging, enabling students to apply their skills effectively.
- Worksheets and PDFs: Downloadable worksheets allow for offline practice, which is particularly useful for self-study or homework assignments.
- Exam-style Problems: Corbettmaths incorporates questions modeled after exam papers, ensuring that students are well-prepared for real tests.
Benefits of Using Corbettmaths for Simultaneous Equations
- Comprehensive Coverage: Corbettmaths covers all aspects of simultaneous equations, from linear systems to more complex non-linear cases. This makes it suitable for learners of all skill levels.
- User-friendly Design: The resources are organized intuitively, allowing users to easily navigate and access the content they need. The structured approach ensures a smooth learning experience.
- Free Access: Most resources on Corbettmaths are free, making it an accessible option for students and teachers alike.
- Interactive Learning: The combination of videos, practice questions, and worksheets engages learners and promotes active participation.
- Feedback and Solutions: The platform provides detailed solutions to problems, allowing students to understand their mistakes and learn from them.
How to Utilize Corbettmaths for Simultaneous Equations
- Start with Tutorials: Begin by watching the video tutorials to understand the concepts. Pay attention to the steps used in solving simultaneous equations.
- Practice Regularly: Download the worksheets and solve them consistently. Start with easier questions to build confidence, then progress to more challenging problems.
- Review Solutions: After completing the exercises, review the provided solutions on Corbettmaths to ensure your answers are correct and understand any errors.
- Simulate Exam Conditions: Use the exam-style questions to practice under timed conditions. This helps improve speed and accuracy.
- Repeat and Reinforce: Revisit the materials periodically to reinforce your understanding. The repetitive practice will help solidify your skills.
Sample Question from Corbettmaths
Here’s an example of a practice question you might find on Corbettmaths:
Solve the following simultaneous equations:
4x+3y=184x + 3y = 184x+3y=18
2x−y=42x – y = 42x−y=4
Solution:
Using the elimination method: Multiply the second equation by 3: 6x−3y=126x – 3y = 126x−3y=12. Add the equations: (4x+3y)+(6x−3y)=18+12(4x + 3y) + (6x – 3y) = 18 + 12(4x+3y)+(6x−3y)=18+12. 10x=3010x = 3010x=30. x=3x = 3x=3. Substitute x=3x = 3x=3 into 2x−y=42x – y = 42x−y=4: 2(3)−y=42(3) – y = 42(3)−y=4. y=2y = 2y=2. The solution is x=3x = 3x=3 and y=2y = 2y=2.
Why Practice Simultaneous Equations?
Simultaneous equations are vital in various real-life applications, including:
- Physics: Solving problems involving forces and motion.
- Economics: Analyzing supply and demand models.
- Engineering: Calculating unknown values in circuit analysis.
Developing proficiency in this topic not only aids in academic success but also enhances critical thinking and problem-solving abilities.
Conclusion
Mastering simultaneous equations is a crucial step in mathematics education, and Corbettmaths is a valuable resource for achieving this goal. With its well-structured tutorials, varied practice questions, and user-friendly interface, the platform makes learning accessible and effective for all students. By utilizing the resources provided by Corbettmaths, students can confidently tackle simultaneous equations and excel in both exams and real-world applications.